Coordinate Geometry ⇒⇒ Exercise 7.1

Question 1 (i)

Find the distance between the following pairs of points:
(i) (2, 3), (4, 1)

Solution :

Let the two point be A (2, 3) and B (4,1) .

We need to find distance AB

( We know that, in a plane distance between two given points AB = $\sqrt{ (x_2 - x_1)^2 + (y_2 - y_1)^2 }$ )

Here, x coordinate of point A = x₁ = 2

And, y coordinate of point A = y₁ = 3

Here, x coordinate of point B = x₂ = 4

And, y coordinate of point B = y₂ = 1

Putting Values in formula :

$$⇒ \sqrt{ (4 - 2)^2 + (1 - 3)^2 }$$

$$⇒ \sqrt{ (2)^2 + ( - 2)^2 }$$

$$⇒ \sqrt{ 4 + 4 }$$

$$⇒ \sqrt{8 }$$

$$⇒ 2\sqrt{2 }$$

Thus, distance between given points = $ 2\sqrt{2}$ unit .

Question 1 (ii)

Find the distance between the following pairs of points:
(ii) (–5, 7), (–1, 3)

Solution :

Let the two point be A (–5, 7) and B (–1, 3)) .

We need to find distance AB

( We know that, in a plane distance between two given points AB = $\sqrt{ (x_2 - x_1)^2 + (y_2 - y_1)^2 }$ )

Here, x coordinate of point A = x₁ = -5

And, y coordinate of point A = y₁ = 7

Here, x coordinate of point B = x₂ = -1

And, y coordinate of point B = y₂ = 3

Putting Values in formula :

$$⇒ \sqrt{ (-1 - (-5))^2 + (3 - 7)^2 }$$

$$⇒ \sqrt{ (-1 + 5)^2 + (- 4)^2 }$$

$$⇒ \sqrt{ (4)^2 + (- 4)^2 }$$

$$⇒ \sqrt{ 16 + 16 }$$

$$⇒ \sqrt{32 }$$

$$⇒ \sqrt{16 × 2 }$$

$$⇒ 4\sqrt{2 }$$

Thus, distance between given points = $ 4\sqrt{2}$ unit.

Question 1 (iii)

Find the distance between the following pairs of points:
(iii) (a, b), (–a, –b)

Solution :

Let the two point be P (a, b) and Q (–a, –b) .

We need to find distance PQ

( We know that, in a plane distance between two given points AB = $\sqrt{ (x_2 - x_1)^2 + (y_2 - y_1)^2 }$ )

Here, x coordinate of point P = x₁ = a

And, y coordinate of point P = y₁ = b

Here, x coordinate of point Q = x₂ = -a

And, y coordinate of point Q = y₂ = -b

Putting Values in formula :

$$\sqrt{ (-a - a)^2 + (-b - b)^2 }$$

$$⇒ \sqrt{ (-2a)^2 + (- 2b)^2 }$$

$$⇒ \sqrt{ 4a^2 + 4b^2 }$$

$$⇒ \sqrt{ 4 (a^2 + b^2 ) }$$

$$⇒ 2\sqrt{ (a^2 + b^2 ) } $$

Thus, distance between given points = $ 2\sqrt{(a^2 + b^2 )}$ unit .

Question 2

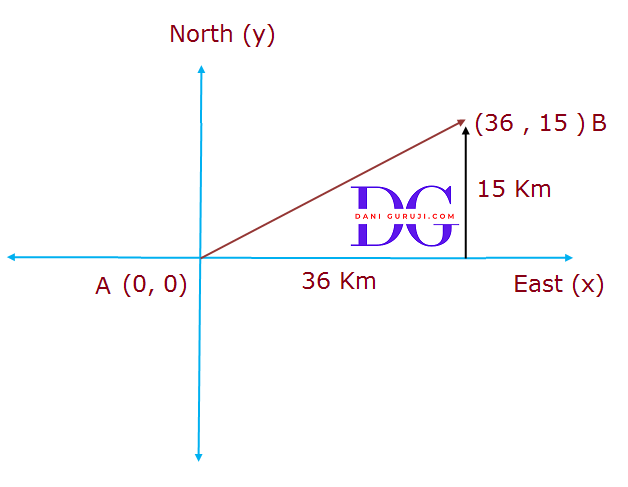
Find the distance between the points (0, 0) and (36, 15). Can you now find the distance between the two towns A and B discussed in Section 7.2 .

Solution :

Let the two point be A (0, 0) and B (36, 15).

We need to find distance AB

( We know that, in a plane distance between two given points AB = $\sqrt{ (x_2 - x_1)^2 + (y_2 - y_1)^2 }$ )

Here, x coordinate of point A = x₁ = 0

And, y coordinate of point A = y₁ = 0

Here, x coordinate of point B = x₂ = 36

And, y coordinate of point B = y₂ = 15

Putting Values in formula :

$$\sqrt{ (36 - 0)^2 + (15 - 0)^2 }$$

$$⇒ \sqrt{ (36)^2 + (15)^2 }$$

$$⇒ \sqrt{ 1296 + 225 }$$

$$⇒ \sqrt{ 1521 }$$

$$⇒ 39 unit $$

Yes, we can find the distance between the given towns A and B.

Let us take town A at origin point (0,0)Hence, town B will be at point (36,15) with respect to town A And, as calculated above, the distance between town A and B will be 39 km .

Question 3

Determine if the points (1, 5), (2, 3) and (– 2, – 11) are collinear.

Solution :

Let the three point be P , Q and R .

Three or more points are said to be collinear if they lie on a single straight line.

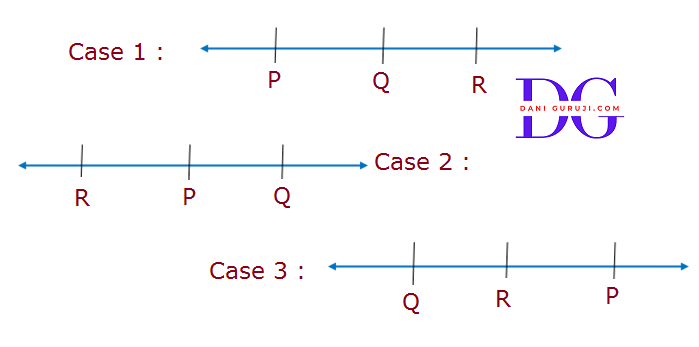
There are three case possible

Case 1 : P,Q and R collinear if

PQ + QR = PR

Case 2 : P,Q and R collinear if

PR + PQ = RQ

Case 3 : P,Q and R collinear if

QR + PR = PQ

Let the three point be P (1, 5) and Q (2, 3) , R(– 2, – 11) .

We need to find distance between P (1, 5) and Q (2, 3)

( We know that, in a plane distance between two given points AB = $\sqrt{ (x_2 - x_1)^2 + (y_2 - y_1)^2 }$ )

Here, x coordinate of point P = x₁ = 1

And, y coordinate of point P = y₁ = 5

Here, x coordinate of point Q = x₂ = 2

And, y coordinate of point Q = y₂ = 3

Putting Values in formula :

$$\sqrt{ (2 - 1)^2 + (3 - 5)^2 }$$

$$⇒ \sqrt{ (1)^2 + (- 2)^2 }$$

$$⇒ \sqrt{ 1 + 4 }$$

$$ PQ = \sqrt{ 5 }$$

Now, to find distance between Q (2, 3) and R(– 2, – 11)

Here, x coordinate of point Q = x₁ = 2

And, y coordinate of point Q = y₁ = 3

Here, x coordinate of point R = x₂ = -2

And, y coordinate of point R = y₂ = -11

Putting Values in formula :

$$\sqrt{ (-2 - 2)^2 + (-11 - 3)^2 }$$

$$⇒ \sqrt{ (-4)^2 + (- 14)^2 }$$

$$⇒ \sqrt{ 16 + 196 }$$

$$ QR = \sqrt{ 212 }$$

Now, to find distance between P (1, 5) and R(– 2, – 11)

Here, x coordinate of point P = x₁ = 1

And, y coordinate of point P = y₁ = 5

Here, x coordinate of point R = x₂ = -2

And, y coordinate of point R = y₂ = -11

Putting Values in formula :

$$\sqrt{ (-2 - 1)^2 + (-11 - 5)^2 }$$

$$⇒ \sqrt{ (-3)^2 + (- 16)^2 }$$

$$⇒ \sqrt{ 9 + 256 }$$

$$ PR = \sqrt{ 265 }$$

Since PQ + QR $ \ne$ PR

And PR + PQ $ \ne$ RQ

And QR + PR $ \ne$ PQ

As three of the cases are not satisfied. Hence the points are not collinear.

Question 4

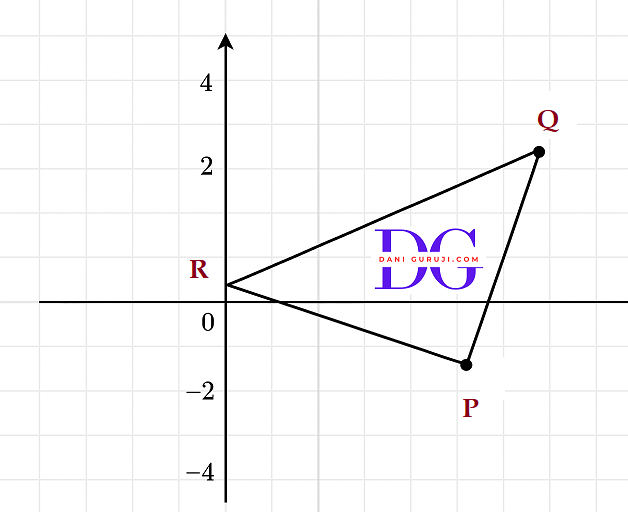
Check whether (5, -2), (6, 4) and (7, – 2) are the vertices of an isosceles triangle.

Solution :

Let us assume that points P , Q and R are representing the vertices of the given triangle respectively as shown in the figure.

To determine if the points (5,-2), (6,4), and (7,−2) are the vertices of an isosceles triangle, we must check if any two sides of the triangle have the same length. We can do this by calculating the distance between each pair of points using the distance formula:

There are only One case possible in order to be isosceles

Case 1 : if PQ = PR

Or

Case 2 : if PQ = QR

Or

Case 3 : if QR = PR

Let the three point be P (5, -2) and Q (6, 4) , R(7, – 2) .

We need to find distance between P (5, 2) and Q (6, 4)

( We know that, in a plane distance between two given points AB = $\sqrt{ (x_2 - x_1)^2 + (y_2 - y_1)^2 }$ )

Here, x coordinate of point P = x₁ = 5

And, y coordinate of point P = y₁ = -2

Here, x coordinate of point Q = x₂ = 6

And, y coordinate of point Q = y₂ = 4

Putting Values in formula :

$$\sqrt{ (6 - 5)^2 + (4 - (-2))^2 }$$

$$⇒ \sqrt{ (1)^2 + ( 6)^2 }$$

$$⇒ \sqrt{ 1 + 36 }$$

$$ PQ = \sqrt{ 37 }$$

Now, to find distance between Q (6, 4) and R(7, – 2)

Here, x coordinate of point Q = x₁ = 6

And, y coordinate of point Q = y₁ = 4

Here, x coordinate of point R = x₂ = 7

And, y coordinate of point R = y₂ = -2

Putting Values in formula :

$$\sqrt{ (7 - 6)^2 + (-2 - 4)^2 }$$

$$⇒ \sqrt{ (1)^2 + (- 6)^2 }$$

$$⇒ \sqrt{ 1 + 36 }$$

$$ QR = \sqrt{ 37 }$$

Now, to find distance between P (5, -2) and R(7, – 2)

Here, x coordinate of point P = x₁ = 5

And, y coordinate of point P = y₁ = -2

Here, x coordinate of point R = x₂ = 7

And, y coordinate of point R = y₂ = -2

Putting Values in formula :

$$\sqrt{ (7 - 5)^2 + (-2 - (-2))^2 }$$

$$⇒ \sqrt{ (2)^2 + (0)^2 }$$

$$⇒ \sqrt{ 4 }$$

$$ PR = 2 $$

Since the lengths of two sides, PQ and QR , are both equal to $\sqrt 37$ , the triangle is isosceles.

Question 5

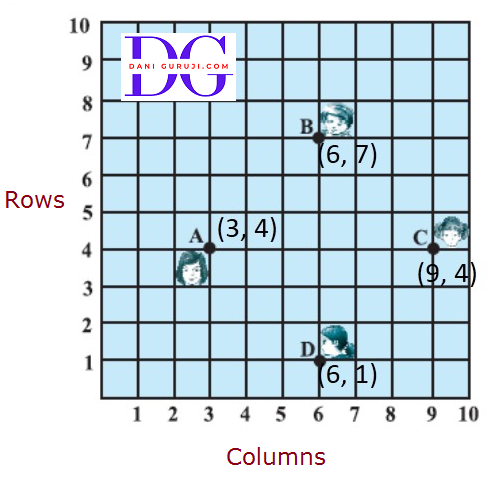
In a classroom, 4 friends areseated at the points A, B, C and D as shown in Figure Champa and Chameli walk into the class and after observing for a few minutes Champa asks Chameli, “Don’t you think ABCD is a square?” Chameli disagrees. Using distance formula, find which of them is correct

Solution :

It can be seen that A (3, 4), B (6, 7), C (9, 4), and D (6, 1) are the positions of 4 friends

To check whether the given points are Square or not , the distance of the four sides should be equal and the length of the two diagonals should be the same.

Hence we have to prove :

AB = BC = CD = AD

And

AC = BD

Let the four point be A (3, 4), B (6, 7), C (9, 4), and D (6, 1).

We need to find distance between A (3, 4) and B (6, 7)

( We know that, in a plane distance between two given points AB = $\sqrt{ (x_2 - x_1)^2 + (y_2 - y_1)^2 }$ )

Here, x coordinate of point A = x₁ = 3

And, y coordinate of point A = y₁ = 4

Here, x coordinate of point B = x₂ = 6

And, y coordinate of point B = y₂ = 7

Putting Values in formula :

$$\sqrt{ (6 - 3)^2 + (7 - 4)^2 }$$

$$⇒ \sqrt{ (3)^2 + ( 3)^2 }$$

$$⇒ \sqrt{ 9 + 9 }$$

$$⇒ \sqrt{ 18 }$$

$$ AB = 3\sqrt{ 2 }$$

Similarly, to find distance between B (6, 7), and C (9, 4)

Here, x coordinate of point B = x₁ = 6

And, y coordinate of point B = y₁ = 7

Here, x coordinate of point C = x₂ = 9

And, y coordinate of point C = y₂ = 4

Putting Values in formula :

$$\sqrt{ (9 - 6)^2 + (4 - 7)^2 }$$

$$⇒ \sqrt{ (3)^2 + (-3)^2 }$$

$$⇒ \sqrt{ 9 + 9 }$$

$$⇒ \sqrt{ 18 }$$

$$ BC = 3\sqrt{ 2 }$$

Similarly, to find distance between C (9, 4) and D (6, 1)

Here, x coordinate of point C = x₁ = 9

And, y coordinate of point C = y₁ = 4

Here, x coordinate of point D = x₂ = 6

And, y coordinate of point D = y₂ = 1

Putting Values in formula :

$$\sqrt{ (6 - 9)^2 + (1 - 4)^2 }$$

$$⇒ \sqrt{ (-3)^2 + (-3)^2 }$$

$$⇒ \sqrt{ 9 + 9 }$$

$$⇒ \sqrt{ 18 }$$

$$ CD = 3\sqrt{ 2 }$$

Similarly, to find distance between A (3, 4) and D (6, 1)

Here, x coordinate of point A = x₁ = 3

And, y coordinate of point A = y₁ = 4

Here, x coordinate of point D = x₂ = 6

And, y coordinate of point D = y₂ = 1

Putting Values in formula :

$$\sqrt{ (6 - 3)^2 + (1 - 4)^2 }$$

$$⇒ \sqrt{ (3)^2 + (-3)^2 }$$

$$⇒ \sqrt{ 9 + 9 }$$

$$⇒ \sqrt{ 18 }$$

$$ AD = 3\sqrt{ 2 }$$

Finding the diagonals AC .To find distance between A (3, 4) and C (9, 4)

Here, x coordinate of point A = x₁ = 3

And, y coordinate of point A = y₁ = 4

Here, x coordinate of point C = x₂ = 9

And, y coordinate of point C = y₂ = 4

Putting Values in formula :

$$\sqrt{ (9 - 3)^2 + (4 - 4)^2 }$$

$$⇒ \sqrt{ (6)^2 + (0)^2 }$$

$$⇒ \sqrt{ 36 + 0 }$$

$$⇒ \sqrt{ 36 }$$

$$ AC = 6 $$

Finding the diagonals BD. To find distance between B (6, 7), and D (6, 1)

Here, x coordinate of point B = x₁ = 6

And, y coordinate of point B = y₁ = 7

Here, x coordinate of point D = x₂ = 6

And, y coordinate of point D = y₂ = 1

Putting Values in formula :

$$\sqrt{ (6 - 6)^2 + (1 - 7)^2 }$$

$$⇒ \sqrt{ (0)^2 + (-6)^2 }$$

$$⇒ \sqrt{ 0 + 36 }$$

$$⇒ \sqrt{ 36 }$$

$$ BD = 6 $$

Since AB = BC = CD = AD and AC= BD, it satisfies the condition of square

Therefore ABCD is a square, and hence, Champa was correct

Question 6 (i)

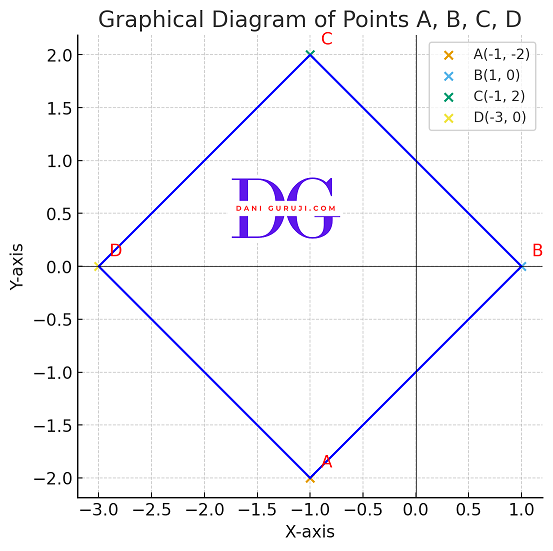
Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer.
(i) (-1, -2), (1, 0), (-1, 2), (-3,0)

Solution :

Let the four point be A (-1, -2), B (1, 0), C (-1, 2), and D (-3,0).

Then, it is to detect that which type of quadrilateral is formed by these points.

(1)We need to find distance between A (-1, -2) and B (1, 0)

( We know that, in a plane distance between two given points AB = $\sqrt{ (x_2 - x_1)^2 + (y_2 - y_1)^2 }$ )

Here, x coordinate of point A = x₁ = -1

And, y coordinate of point A = y₁ = -2

Here, x coordinate of point B = x₂ = 1

And, y coordinate of point B = y₂ = 0

Putting Values in formula :

$$\sqrt{ (1 - (-1))^2 + (0 - (-2))^2 }$$

$$\sqrt{ (1 + 1 ))^2 + (0 +2 )^2 }$$

$$⇒ \sqrt{ (2)^2 + ( 2)^2 }$$

$$⇒ \sqrt{ 4 + 4 }$$

$$⇒ \sqrt{ 8 }$$

$$ AB = 2\sqrt{ 2 }$$

(2) Similarly, to find distance between B (1, 0), and C (-1, 2)

Here, x coordinate of point B = x₁ = 1

And, y coordinate of point B = y₁ = 0

Here, x coordinate of point C = x₂ = -1

And, y coordinate of point C = y₂ = 2

Putting Values in formula :

$$\sqrt{ (-1 - 1)^2 + (2 - 0)^2 }$$

$$⇒ \sqrt{ (-2)^2 + ( 2)^2 }$$

$$⇒ \sqrt{ 4 + 4 }$$

$$⇒ \sqrt{ 8 }$$

$$ BC = 2\sqrt{ 2 }$$

(3) Similarly, to find distance between C (-1, 2) and D (-3,0)

Here, x coordinate of point C = x₁ = -1

And, y coordinate of point C = y₁ = 2

Here, x coordinate of point D = x₂ = -3

And, y coordinate of point D = y₂ = 0

Putting Values in formula :

$$\sqrt{ ((-3) -(-1) )^2 + (0 - 2)^2 }$$

$$\sqrt{ (-3 + 1 ))^2 + (-2 )^2 }$$

$$⇒ \sqrt{ (-2)^2 + ( -2)^2 }$$

$$⇒ \sqrt{ 4 + 4 }$$

$$⇒ \sqrt{ 8 }$$

$$ CD = 2\sqrt{ 2 }$$

(4) Similarly, to find distance between A (-1, -2) and D (-3,0)

Here, x coordinate of point A = x₁ = -1

And, y coordinate of point A = y₁ = -2

Here, x coordinate of point D = x₂ = -3

And, y coordinate of point D = y₂ = 0

Putting Values in formula :

$$\sqrt{ ((-3) -(-1) )^2 + (0 - (-2))^2 }$$

$$\sqrt{ (-3 + 1 ))^2 + (0 + 2 )^2 }$$

$$⇒ \sqrt{ (-2)^2 + ( 2)^2 }$$

$$⇒ \sqrt{ 4 + 4 }$$

$$⇒ \sqrt{ 8 }$$

$$ AD = 2\sqrt{ 2 }$$

Since AB = BC = CD = AD = $ 2\sqrt{ 2 }$

Here ABCD can be a square or rhombus ,Therefore we find the length of diagonals AC and BD

(5) Finding the diagonals AC . To find distance between A (-1, -2) and C (-1, 2)

Here, x coordinate of point A = x₁ = -1

And, y coordinate of point A = y₁ = -2

Here, x coordinate of point C = x₂ = -1

And, y coordinate of point C = y₂ = 2

Putting Values in formula :

$$\sqrt{ (-1 - (-1))^2 + (2 - (-2))^2 }$$

$$\sqrt{ (-1 + 1)^2 + (2 + 2)^2 }$$

$$⇒ \sqrt{ (0)^2 + ( 4)^2 }$$

$$⇒ \sqrt{ 16 }$$

$$ AC = 4 $$

(6) Finding the diagonals BD. To find distance between B (1, 0), and D (-3, 0)

Here, x coordinate of point B = x₁ = 1

And, y coordinate of point B = y₁ = 0

Here, x coordinate of point D = x₂ = -3

And, y coordinate of point D = y₂ = 0

Putting Values in formula :

$$\sqrt{ ((-3) -1 )^2 + (0 - 0)^2 }$$

$$\sqrt{ (-3 - 1 ))^2 + (0 )^2 }$$

$$⇒ \sqrt{ (-4)^2 + ( 0)^2 }$$

$$⇒ \sqrt{ 16 }$$

$$ BD = 4$$

Since AB = BC = CD = AD = $ 2\sqrt{ 2 }$

All sides of quadrilateral are equal.

And AC = Bd = 4

Both diagonals are equal

Hence, All sides of quadrilateral and both diagonals are equal.

Therefore ABCD is a Square.

Question 6 (ii)

Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer.
(ii) (-3, 5), (3, 1), (0, 3), (-1,-4)

Solution :

Let the four point be A (-3, 5), B(3, 1), C (0, 3), and D (-1,-4).

Then, it is to detect that which type of quadrilateral is formed by these points.

(1)We need to find distance between A (-3, 5) and B(3, 1)

( We know that, in a plane distance between two given points AB = $\sqrt{ (x_2 - x_1)^2 + (y_2 - y_1)^2 }$ )

Here, x coordinate of point A = x₁ = -3

And, y coordinate of point A = y₁ = 5

Here, x coordinate of point B = x₂ = 3

And, y coordinate of point B = y₂ = 1

Putting Values in formula :

$$\sqrt{ (3 - (-3))^2 + (1 - 5)^2 }$$

$$\sqrt{ (3 + 3 ))^2 + (-4 )^2 }$$

$$⇒ \sqrt{ (6)^2 + ( -4)^2 }$$

$$⇒ \sqrt{ 36 + 16 }$$

$$⇒ \sqrt{ 52 }$$

$$ AB = \sqrt{ 52 }$$

(2) Similarly, to find distance between B(3, 1), and C (0, 3)

Here, x coordinate of point B = x₁ = 3

And, y coordinate of point B = y₁ = 1

Here, x coordinate of point C = x₂ = 0

And, y coordinate of point C = y₂ = 3

Putting Values in formula :

$$\sqrt{ (0 - 3)^2 + (3 - 1)^2 }$$

$$⇒ \sqrt{ (-3)^2 + ( 2)^2 }$$

$$⇒ \sqrt{ 9 + 4 }$$

$$⇒ \sqrt{ 13 }$$

$$ BC = \sqrt{ 13 }$$

(3) Similarly, to find distance between C (0, 3) and D (-1,-4)

Here, x coordinate of point C = x₁ = 0

And, y coordinate of point C = y₁ = 3

Here, x coordinate of point D = x₂ = -1

And, y coordinate of point D = y₂ = -4

Putting Values in formula :

$$\sqrt{ ((-1) - 0 )^2 + (-4 - 3)^2 }$$

$$\sqrt{ (-1 ))^2 + (-7)^2 }$$

$$⇒ \sqrt{ 1 + 49 }$$

$$⇒ \sqrt{ 50}$$

$$ CD = \sqrt{ 50 }$$

(4) Similarly, to find distance between A (-3, 5) and D (-1,-4)

Here, x coordinate of point A = x₁ = -3

And, y coordinate of point A = y₁ = 5

Here, x coordinate of point D = x₂ = -1

And, y coordinate of point D = y₂ = - 4

Putting Values in formula :

$$\sqrt{ ((-1) -(-3) )^2 + (-4 - 5)^2 }$$

$$\sqrt{ (-1 + 3 ))^2 + (-9 )^2 }$$

$$⇒ \sqrt{ (-2)^2 + ( -9)^2 }$$

$$⇒ \sqrt{ 4 + 81 }$$

$$⇒ \sqrt{ 85 }$$

$$ AD = \sqrt{85}$$

Here, AB =$ \sqrt{ 52 } $ , BC = $ \sqrt{ 13 } $ , CD =$ \sqrt{ 50 } $ , AD = $ \sqrt{ 85 }$

Since AB $ \ne $ BC $ \ne $ CD $ \ne $ AD

It can be observed that all sides of this quadrilateral are of different lengths.

It’s also seen that points A, B and C are collinear. So, the given points can only form 3 sides, i.e. a triangle and not a quadrilateral which has 4 sides.

Question 6 (iii)

Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer.
(iii) (4, 5), (7, 6), (4, 3), (1, 2)

Solution :

Let the four point be A (4, 5), B (7, 6), C (4, 3), and D (1, 2).

Then, it is to detect that which type of quadrilateral is formed by these points.

(1)We need to find distance between A (4, 5) and B (7, 6)

( We know that, in a plane distance between two given points AB = $\sqrt{ (x_2 - x_1)^2 + (y_2 - y_1)^2 }$ )

Here, x and y coordinate of point A , x₁ = 4 and y₁ = 5

And, x and y coordinate of point B, x₂ = 7 and y₂ = 6

Putting Values in distance formula :

$$\sqrt{ (7 - 4)^2 + (6 - 5)^2 }$$

$$\sqrt{ (3 ))^2 + (1 )^2 }$$

$$⇒ \sqrt{ 9 + 1 }$$

$$⇒ \sqrt{ 10 }$$

$$ AB = \sqrt{ 10 }$$

(2) Similarly, to find distance between B (7, 6), and C (4, 3)

Here, x and y coordinate of point B , x₁ = 7 and y₁ = 6

And, x and y coordinate of point C , x₂ = 4 and y₂ = 3

Putting Values in distance formula :

$$\sqrt{ (4 - 7)^2 + (3 - 6)^2 }$$

$$⇒ \sqrt{ (-3)^2 + (-3)^2 }$$

$$⇒ \sqrt{ 9 + 9 }$$

$$⇒ \sqrt{ 18 }$$

$$ BC = \sqrt{ 18 }$$

(3) Similarly, to find distance between C (4, 3) and D (1, 2)

Here, x and y coordinate of point C , x₁ = 4 and y₁ = 3

And, x and y coordinate of point D , x₂ = 1 and y₂ = 2

Putting Values in distance formula :

$$\sqrt{ (1 - 4 )^2 + (2 - 3)^2 }$$

$$\sqrt{ (-3 ))^2 + (-1)^2 }$$

$$⇒ \sqrt{ 9 + 1 }$$

$$⇒ \sqrt{ 10}$$

$$ CD = \sqrt{ 10 }$$

(4) Similarly, to find distance between A (4, 5) and D (1, 2)

Here, x and y coordinate of point A , x₁ = 4 and y₁ = 5

And, x and y coordinate of point D , x₂ = 1 and y₂ = 2

Putting Values in distance formula :

$$\sqrt{ (1 - 4 )^2 + (2 - 5)^2 }$$

$$\sqrt{ (- 3 ))^2 + (-3 )^2 }$$

$$⇒ \sqrt{ 9 + 9 }$$

$$⇒ \sqrt{ 18 }$$

$$ AD = \sqrt{18}$$

Here, AB and CD = $ \sqrt{ 10 }$

And, BC and AD = $ \sqrt{ 18 } $

Since both pairs of opposite side of quadrilateral are equal , it would be a parallelogram .

Question 7

Find the point on the x-axis which is equidistant from (2, − 5) and (− 2, 9).

Solution :

We have to find a point on x-axis. Therefore, its y-coordinate will be 0, So it's co-ordinates are (x,0).

and assuming x= a

Let given coordinates are A(2, –5), B (–2, 9) and P(a, 0) is on the x-axis.

Since, point P is equidistanct from the given coordinates,

thus AP = BP

( We know that, in a plane distance between two given points AB = $\sqrt{ (x_2 - x_1)^2 + (y_2 - y_1)^2 }$ )

(1)To find distance between A (2, -5) and P (a, 0)

Here, x and y coordinate of point A , x₁ = 2 and y₁ = -5

And, x and y coordinate of point P, x₂ = a and y₂ = 0

Putting Values in distance formula :

$$\sqrt{ (a - 2)^2 + (0 - (-5))^2 }$$

$$⇒ \sqrt{(a - 2)^2 + (5 )^2 }$$

$$⇒ \sqrt{(a^2 + 2^2 - 2 × a ×2) + 25 }$$

$$⇒ \sqrt{(a^2 + 4 - 4a )+ 25 }$$

$$⇒ \sqrt{a^2 - 4a + 29 }$$

$$ AP = \sqrt{a^2 - 4a + 29 }$$

(2) Similarly, to find distance between B (–2, 9) and P (a, 0)

Here, x and y coordinate of point B , x₁ = -2 and y₁ = 9

And, x and y coordinate of point P, x₂ = a and y₂ = 0

Putting Values in distance formula :

$$\sqrt{ (a - (-2))^2 + (0 - 9)^2 }$$

$$⇒ \sqrt{(a + 2)^2 + (-9 )^2 }$$

$$⇒ \sqrt{(a^2 + 2^2 + 2 × a ×2) + 81 }$$

$$⇒ \sqrt{(a^2 + 4 + 4a )+ 81 }$$

$$⇒ \sqrt{a^2 + 4a + 85 }$$

$$ BP = \sqrt{a^2 + 4a + 85 }$$

From the question AP = BP

$$⇒ {\sqrt{a^2 - 4a + 29 }} = {\sqrt{a^2 + 4a + 85 }} $$

Squaring both Sides

$$⇒ (\sqrt{a^2 - 4a + 29 })^2 = (\sqrt{a^2 + 4a + 85 })^2 $$

$$⇒ {a^2 - 4a + 29 } = {a^2 + 4a + 85 } $$

$$⇒ {a^2 - a^2 - 4a - 4a } = { 85 - 29 } $$

$$⇒ { - 8a } = { 56} $$

$$⇒ a = { 56 \over {-8} }$$

$$⇒ a = -7 $$

Here is required point P (-7 , 0)

Therefore, the point equidistant from the given points on the axis is (−7,0).

Question 8

Find the values of y for which the distance between the points P (2, − 3) and Q (10, y) is 10 units.

Solution :

Let given coordinates are P (2, − 3) and Q (10, y).

And, PQ = 10 unit

( We know that, in a plane distance between two given points PQ = $\sqrt{ (x_2 - x_1)^2 + (y_2 - y_1)^2 }$ )

To find distance between P (2, − 3) and Q (10, y)

Here, x and y coordinate of point P , x₁ = 2 and y₁ = -3

And, x and y coordinate of point Q, x₂ = 10 and y₂ = y

Putting Values in distance formula :

$$ PQ = {\sqrt{ (10 - 2)^2 + (y - (-3))^2 }}$$

$$⇒ 10 = {\sqrt{ (8)^2 + (y + 3)^2 }}$$

Squaring both Sides

$$⇒ 10^2 = ({\sqrt{ (8)^2 + (y + 3)^2 }})^2 $$

$$⇒ 100 = {{ 64 + (y + 3)^2 }}$$

$$⇒ 100 = {{ 64 + (y^2 + 3^2 + 2 × y ×3) }}$$

$$⇒ 100 = {{ 64 + y^2 + 9 + 6y }}$$

$$⇒ 0 = { 73 + y^2 + 6y - 100 }$$

$$⇒ 0 = { y^2 + 6y - 27 }$$

By expanding middle term. Here 6y can be written as 9y -3y

$$⇒ 0 = { y^2 + 9y -3y - 27 }$$

By taking common,

$$⇒ 0 = { y(y + 9) -3(y + 9)}$$

$$⇒ 0 = { (y + 9) (y -3)}$$

Here, y + 9 = 0 or y - 3 = 0

Therefore, y = - 9 or y = 3 are the possible values for y

Question 9

If Q (0, 1) is equidistant from P (5, − 3) and R (x, 6), find the values of x. Also find the distance QR and PR.

Solution :

Let given coordinates are P (5, − 3) and R (x, 6).

Since, point Q (0, 1) is equidistanct from the given coordinates,

This means QP = QR

Thus, value of x = ?

And, QR and PR = ?

( We know that, in a plane distance between two given points PQ = $\sqrt{ (x_2 - x_1)^2 + (y_2 - y_1)^2 }$ )

(1)To find distance between Q (0, 1) and P (5, − 3)

Here, x and y coordinate of point Q , x₁ = 0 and y₁ = 1

And, x and y coordinate of point P, x₂ = 5 and y₂ = -3

Putting Values in distance formula :

$$\sqrt{ (5 - 0)^2 + ((-3) - 1 )^2 }$$

$$⇒ \sqrt{(5)^2 + (-4 )^2 }$$

$$⇒ \sqrt{ 25 + 16 }$$

$$⇒ \sqrt{41 }$$

$$ QP = \sqrt{41 }$$

(2) Similarly, to find distance between Q (0, 1) and R (x, 6)

Here, x and y coordinate of point Q , x₁ = 0 and y₁ = 1

And, x and y coordinate of point R, x₂ = x and y₂ = 6

Putting Values in distance formula :

$$\sqrt{ (x - 0)^2 + (6 - 1 )^2 }$$

$$\sqrt{ (x - 0)^2 + (5)^2 }$$

$$⇒ \sqrt{(x^2 + 0^2 - 2 × x ×0) + 25 }$$

$$⇒ \sqrt{x^2 + 25 }$$

$$ QR = \sqrt{x^2+ 25 }$$

From the question QP = QR

$$⇒ \sqrt{41 } = \sqrt{x^2 + 25 } $$

Squaring both Sides

$$⇒ (\sqrt{41 })^2 = (\sqrt{ x^2+ 25 })^2 $$

$$⇒ {41 } = {x^2 + 25 } $$

$$⇒ {0 } = {x^2 + 25 - 41} $$

$$⇒ {0 } = {x^2 - 16} $$

$$⇒ x^2 = {16 }$$

$$⇒ x = \pm 4 $$

Therefore, the point R (x, 6) is ( 4, 6) or (-4 , 6).

(A) When point R is (4, 6),

Finding QR

$$\sqrt{ (4 - 0)^2 + (6 - 1 )^2 }$$

$$\sqrt{ (4)^2 + (5)^2 }$$

$$⇒ \sqrt{16 + 25 }$$

$$⇒ \sqrt{41 }$$

$$ QR = \sqrt{41 }$$

Finding PR

$$\sqrt{ (4 - 5)^2 + (6 - (-3) )^2 }$$

$$\sqrt{ (-1)^2 + (9)^2 }$$

$$⇒ \sqrt{1 + 81 }$$

$$⇒ \sqrt{82 }$$

$$ PR = \sqrt{82 }$$

(B) When point R is (-4, 6),

Finding QR

$$\sqrt{ (-4 - 0)^2 + (6 - 1 )^2 }$$

$$\sqrt{ (-4)^2 + (5)^2 }$$

$$⇒ \sqrt{16 + 25 }$$

$$⇒ \sqrt{41 }$$

$$ QR = \sqrt{41 }$$

Finding PR

$$\sqrt{ (-4 - 5)^2 + (6 - (-3) )^2 }$$

$$\sqrt{ (-9)^2 + (9)^2 }$$

$$⇒ \sqrt{81 + 81 }$$

$$⇒ \sqrt{162 }$$

$$ PR = \sqrt{162 }$$

Question 10

Find a relation between x and y such that the point (x, y) is equidistant from the point (3, 6) and (− 3, 4).

Solution :

Let given coordinates are P (3, 6) and R (− 3, 4).

Since, point Q (x, y) is equidistanct from the given coordinates,

This means QP = QR

( We know that, in a plane distance between two given points PQ = $\sqrt{ (x_2 - x_1)^2 + (y_2 - y_1)^2 }$ )

(1)To find distance between Q (x, y) and P (3, 6)

Here, x and y coordinate of point Q , x₁ = x and y₁ = y

And, x and y coordinate of point P, x₂ = 3 and y₂ = 6

Putting Values in distance formula :

$$\sqrt{ (3 - x)^2 + (6 - y )^2 }$$

$$ QP = \sqrt{ (3 - x)^2 + (6 - y )^2 }$$

(2) Similarly, to find distance between Q (x, y) and R (-3, 4)

Here, x and y coordinate of point Q , x₁ = x and y₁ = y

And, x and y coordinate of point R, x₂ = -3 and y₂ = 4

Putting Values in distance formula :

$$\sqrt{ (-3 - x)^2 + (4 - y )^2 }$$

$$ QR = \sqrt{ (-3 - x)^2 + (4 - y )^2 }$$

From the question QP = QR

⇒$\sqrt{(3 - x)^2 + (6 - y )^2 }$ = $ \sqrt{ (-3 - x)^2 + (4 - y )^2 } $

Squaring both Sides

⇒$ (\sqrt{(3 - x)^2 + (6 - y )^2 } )^2$ = $(\sqrt{ (-3 - x)^2 + (4 - y )^2 })^2 $

⇒$ (3 - x)^2 + (6 - y )^2 $= $ (-3 - x)^2 + (4 - y )^2 $

⇒$ (3^2 + x^2 - 6x) + (6^2 + y^2 - 12y ) $

$ = (-3^2 + x^2+ 6x ) + (4^2 + y^2- 8y ) $

⇒$ (9 + x^2 - 6x) + (36 + y^2 - 12y ) $

$ = (9 + x^2+ 6x ) + (16 + y^2- 8y ) $

⇒$ (9 + x^2 - 6x) - (9 + x^2+ 6x ) $

$ = (16 + y^2- 8y ) - (36 + y^2 - 12y ) $

⇒ $ -12 x = 16 + y^2- 8y - 36 - y^2 + 12y $

⇒ 0 = 12x + 4y -20

⇒ 0 = 4(3x + y -5)

⇒ 0 = 3x + y -5

Thus, the relation between x and y is given by 3x + 4y - 5 =0